Standard Error vs Standard Deviation: What’s the Difference?

Perhaps you’ve come across the terms “standard deviation” and “standard error” and are wondering what the difference is. What are they used for, and what do they actually mean for data analysts? Well, you’ve come to the right place. Keep reading for a beginner-friendly explanation.

When analyzing and interpreting data, you’re trying to find patterns and insights that can tell you something useful. For example, you might use data to better understand the spending habits of people who live in a certain city. In this case, it most likely wouldn’t be possible to collect the data you need from every single person living in that city—rather, you’d use a sample of data and then apply your findings to the general population. As part of your analysis, it’s important to understand how accurately or closely the sample data represents the whole population. In other words, how applicable are your findings?

This is where statistics like standard deviation and standard error come in. In this post, we’ll explain exactly what standard deviation and standard error mean, as well as the key differences between them. First, though, we’ll set the scene by briefly recapping the difference between descriptive and inferential statistics (as standard deviation is a descriptive statistic, while standard error an inferential statistic). Sound confusing? Don’t worry! All will become clear by the end of this post.

If you’re already familiar with descriptive vs inferential statistics, just use the clickable menu to skip ahead.

1. Quick recap: What is the difference between descriptive and inferential statistics?
2. What is standard deviation?
3. How to calculate standard deviation
4. What is standard error?
5. How to calculate standard error
6. Standard error vs standard deviation: What is the difference?
7. Standard error vs standard deviation: When should you use them?
8. Key takeaways and further reading

Are you ready to explore the difference between standard error and standard deviation? Let’s dive in.

1. What is the difference between descriptive and inferential statistics?

The first main difference between standard deviation and standard error is that standard deviation is a descriptive statistic while standard error is an inferential statistic. So what’s the difference?

Descriptive statistics are used to describe the characteristics or features of a dataset. This includes things like distribution(the frequency of different data points within a data sample—for example, how many people in the chosen population have brown hair, blonde hair, black hair, etc), measures of central tendency (the mean, median, and mode values), and variability (how the data is distributed—for example, looking at the minimum and maximum values within a dataset).

While descriptive statistics simply summarize your data, with inferential statistics, you’re making generalizations about a population (e.g. residents of New York City) based on a representative sample of data from that population. Inferential statistics are often expressed as a probability.

You can learn more about the difference between descriptive and inferential statistics in this guide, but for now, we’ll focus on the topic at hand: Standard deviation vs standard error.

So without further ado: What is standard deviation?

2. What is standard deviation?

As already mentioned, standard deviation is a descriptive statistic, which means it helps you to describe or summarize your dataset. In simple terms, standard deviation tells you, on average, how far each value within your dataset lies from the mean. A high standard deviation means that the values within a dataset are generally positioned far away from the mean, while a low standard deviation indicates that the values tend to be clustered close to the mean. So, in a nutshell, it measures how much “spread” or variability there is within your dataset.

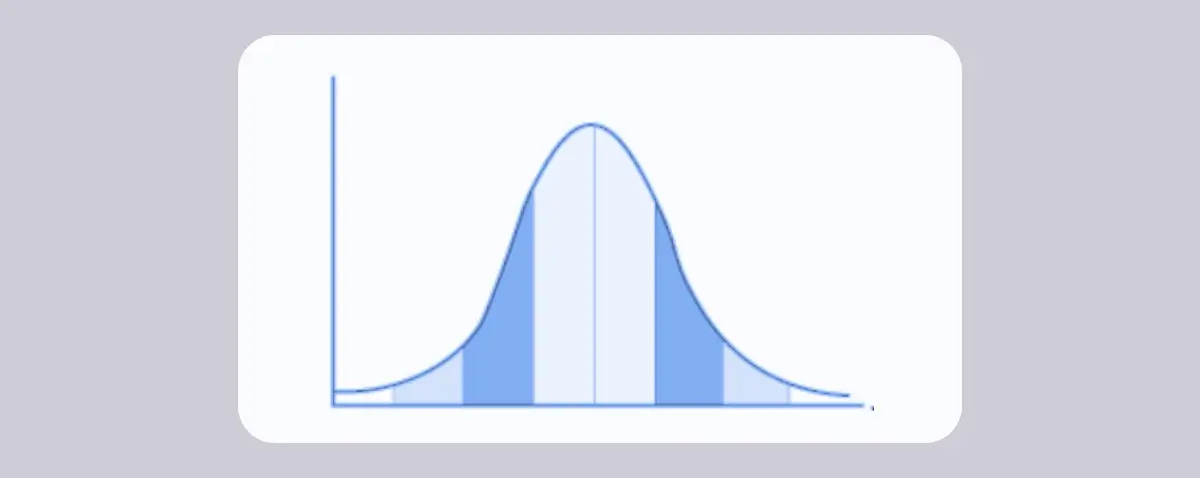
An example of standard deviation

Let’s illustrate this further with the help of an example. Suppose two shops X and Y have four employees each. In shop X, two employees earn $14 per hour and the other two earn $16 per hour. In shop Y, one employee earns $11 per hour, one earns $10 per hour, the third earns $19, and the fourth receives $20 per hour. The average hourly wage for each shop is $15, but you can see that some employees earn much closer to this average value than others.

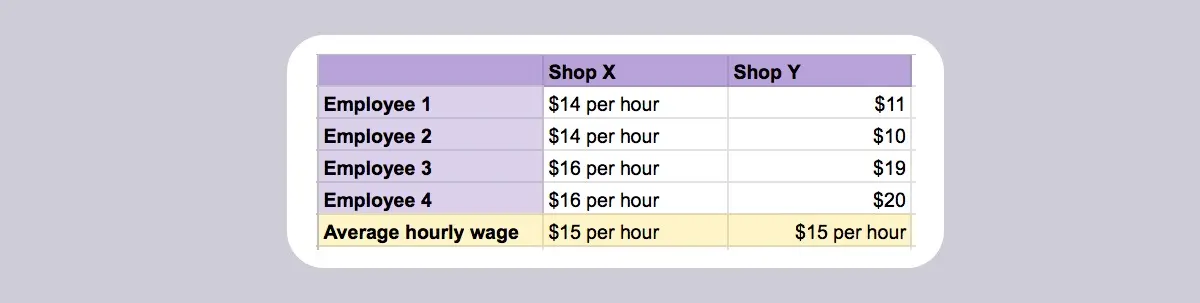
For shop X, the employees’ wages are close to the average value of $15, with little variation (just one dollar difference either side), while for shop Y, the values are spread quite far apart from each other, and from the average. In this simple example, we can see this at a glance without doing any heavy calculations. But, in a more comprehensive and complex dataset, you’d calculate the standard deviation to tell you how far each individual value sits from the mean value.

We’ll look at how to calculate standard deviation in section three. For now, we’ll introduce two key concepts: Normal distribution and the empirical rule.

Normal distribution in standard deviation

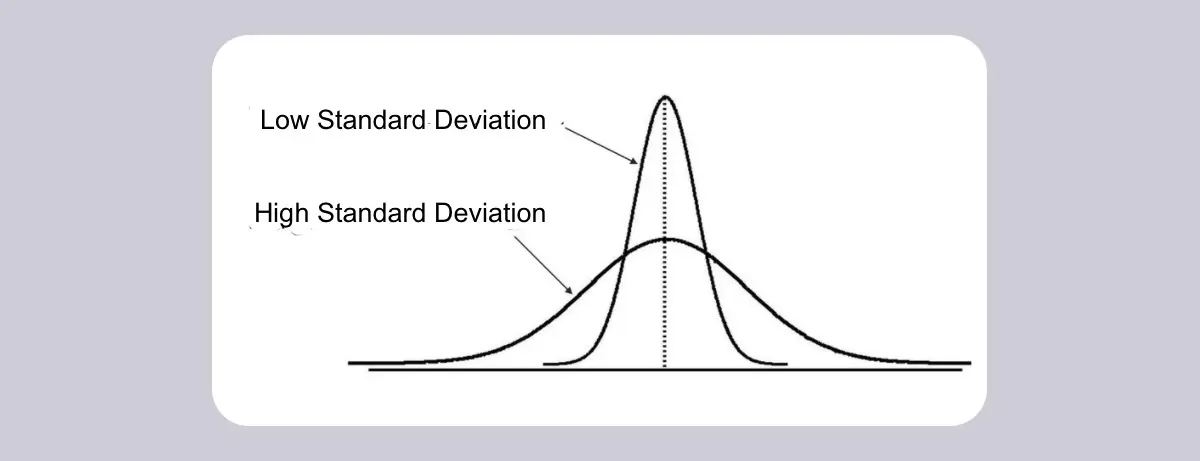
Standard deviation can be interpreted by using normal distribution. In graph form, normal distribution is a bell-shaped curve which is used to display the distribution of independent and similar data values. In any normal distribution, data is symmetrical and distributed in fixed intervals around the mean. In terms of standard deviation, a graph (or curve) with a high, narrow peak and a small spread indicates low standard deviation, while a flatter, broader curve indicates high standard deviation.

What is the empirical rule?

If your dataset follows a normal distribution, you can interpret it using the empirical rule. The empirical rule states that almost all observed data will fall within three standard deviations of the mean:

• Around 68% of values fall within the first standard deviation of the mean
• Around 95% of values fall within the first two standard deviations of the mean
• Around 99.7% of values fall within the first three standard deviations of the mean

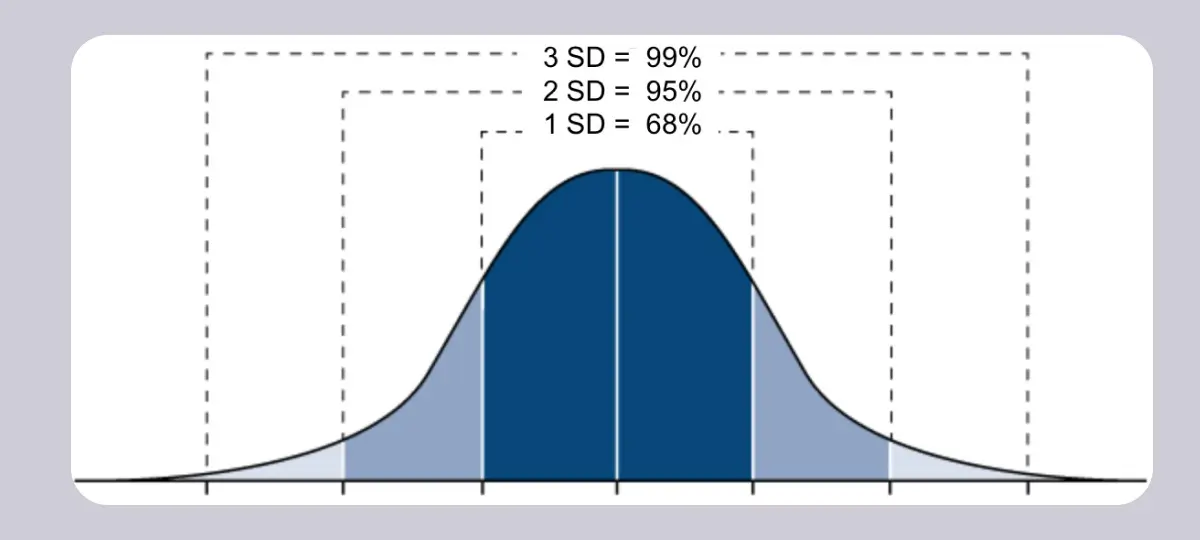
The empirical rule gives a quick overview of data and determines extreme values that don’t follow a pattern of normal distribution.

Now we know what standard deviation tells us, let’s take a look at how to calculate it.

3. How to calculate standard deviation

Now, you must be wondering about the formula used to calculate standard deviation. There are actually two formulas which can be used to calculate standard deviation depending on the nature of the data—are you calculating the standard deviation for population data or for sample data?

• Population data is when you have data for the entire group (or population) that you want to analyze. For example, if you’re collecting data on employees in your company and have data for all 100 employees, you are working with population data.
• Sample data is when you collect data from just a sample of the population you want to gather insights for. For example, if you wanted to collect data on residents of New York City, you’d likely get a sample rather than gathering data for every single person who lives in New York.

With that in mind, you can calculate standard deviation as follows:

How to calculate standard deviation for population data

To calculate standard deviation for population data, the formula is:

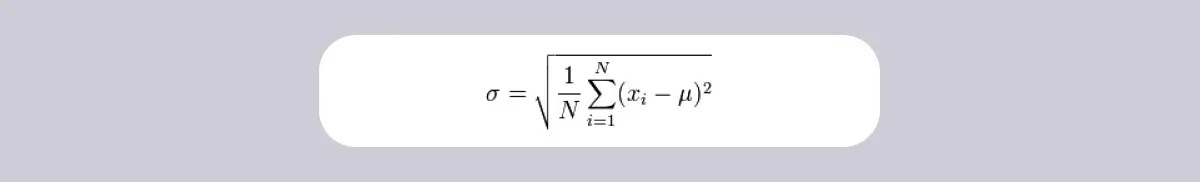Standard deviation vs standard error: Population data[/caption]

Where:

• refers to population standard deviation
• ∑ refers to sum of values
• xi refers to each value
• refers to population mean
• N refers to number of values in the sample

How to calculate standard deviation for sample data

To calculate standard deviation for sample data, you can use the following formula:

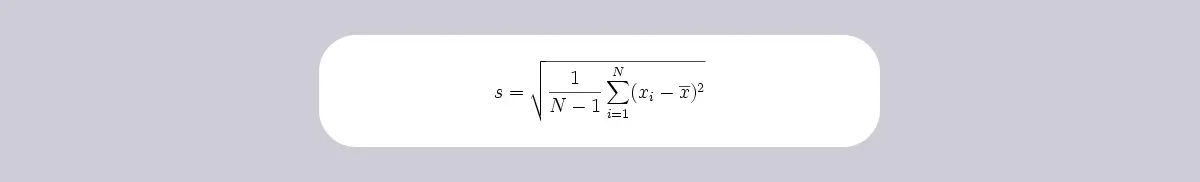
Where:

• s refers to sample standard deviation
• ∑ refers to sum of values
• xi refers to each value
• x̅  refers to sample mean
• N refers to number of values in the sample

At this stage, simply having the mathematical formula may not be all that helpful. Let’s take a look at the actual steps involved in calculating the standard deviation.

How to calculate the standard deviation (step by step)

Here we’ll break down the formula for standard deviation, step by step.

1. Find the mean: Add up all the scores (or values) in your dataset and divide them by the total number of scores or data points.
2. Calculate the deviation from the mean for each individual score or value: Subtract the mean value (from step one) from each individual value or score you have in your dataset. You’ll end up with a set of deviation values.
3. Square each deviation from the mean: Multiply each deviation value you got in step two by itself. E.g. if the deviation value is 4, multiply it by 4.
4. Find the sum of squares: Add up all of the squared deviations as calculated in step three. This will give you a single value known as the sum of squares.
5. Find the variance: Divide the sum of the squares by n − 1 for sample data, or by N for population data. N denotes the total number of scores or values within your dataset, so if you collected data on thirty employees, N is thirty. This will give you a variance value.
6. Find the square root of the variance: Calculate the square root of the variance (as calculated in step five). This gives you the standard deviation (SD).

Let’s further illustrate the step-by-step procedure of calculating standard deviation through an interesting example.

How to calculate standard deviation with an example (in Excel or Google Sheets)

Let’s imagine a group of fifteen employees took part in an assessment, and their employer wants to know how much variation there is in the test scores. Did all employees perform at a similar level, or was there a high standard deviation? The test scores are as follows:

Now let’s calculate the standard deviation for our dataset, following the step-by-step process laid out previously. We’ll use formulas in Google Sheets / Excel, but you can also calculate these values manually.

1. Find the mean: Add all test scores together and divide the total score by the number of scores (1280 / 15 = 85.3). Your mean value is 85.3. In Google Sheets, we used the formula =SUM(A2:A16)/15
2. Calculate the deviation from the mean for each score and then square this value: Subtract the mean value (85.3) from each test score, and then square it. In Google Sheets, we used the formula =(A2-85.3)^2 (and so on). 3
3. Find the sum of the squares: Add up all of the squared deviations (in column B) to find the sum of the squares. In Google Sheets, we used the formula =SUM(B2:B16) to get the value 1139.35.
4. Find the variance: Divide the sum of the squares by N (as we’re using population data). So: 1139.35 / 15 = 75.96.
5. Find the square root of the variance to get the standard deviation: You can calculate the square root in Excel or Google Sheets using the following formula: =B18^0.5. In our example, the square root of 75.96 is 8.7.

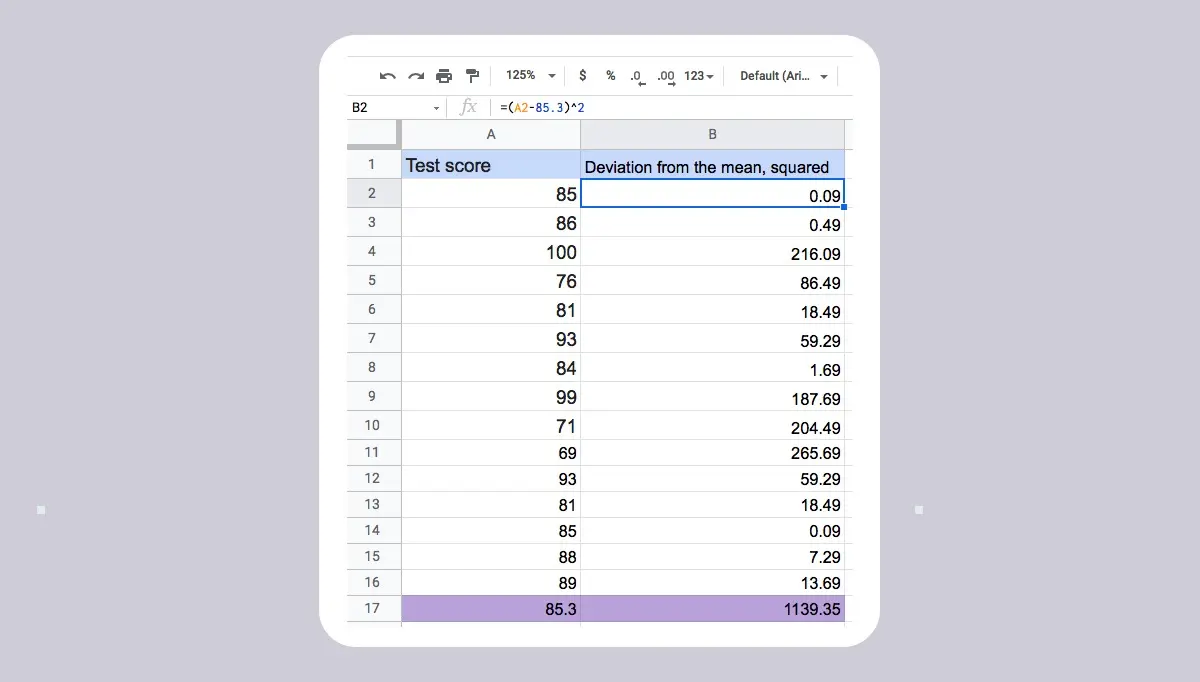
So, for the employee test scores, the standard deviation is 8.7. This is low variance, indicating that all employees performed at a similar level.

4. What is standard error?

Standard error (or standard error of the mean) is an inferential statistic that tells you, in simple terms, how accurately your sample data represents the whole population. For example, if you conduct a survey of people living in New York, you’re collecting a sample of data that represents a segment of the entire population of New York. Different samples of the same population will give you different results, so it’s important to understand how applicable your findings are. So, when you take the mean results from your sample data and compare it with the overall population mean on a distribution, the standard error tells you what the variance is between the two means. In other words, how much would the sample mean vary if you were to repeat the same study with a different sample of people from the New York City population?

Just like standard deviation, standard error is a measure of variability. However, the difference is that standard deviationdescribes variability within a single sample, while standard error describes variability across multiple samples of a population. We’ll explore those differences in more detail in section six. For now, let’s continue to explore standard error.

Standard error can either be high or low. In the case of high standard error, your sample data does not accurately represent the population data; the sample means are widely spread around the population mean. In the case of low standard error, your sample is a more accurate representation of the population data, with the sample means closely distributed around the population mean.

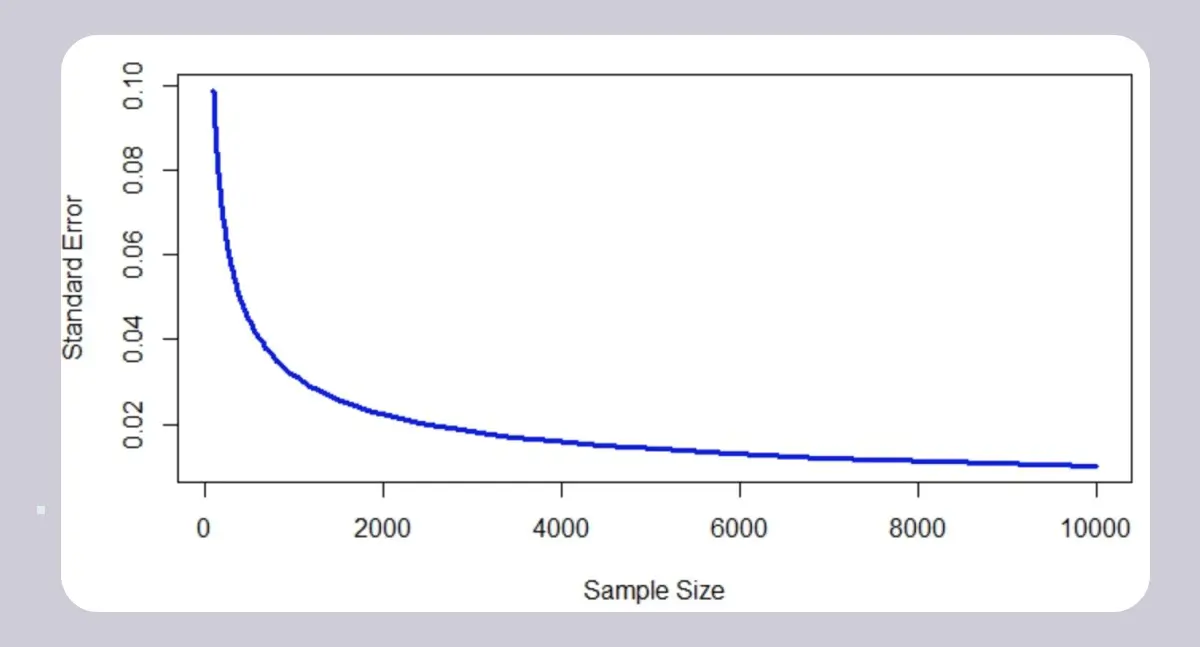
What is the relationship between standard error (SE) and the sample size?

Sample size is inversely proportional to standard error, and so the standard error can be minimized by using a large sample size. As you can see from this graph, the larger the sample size, the lower the standard error.

5. How to calculate standard error

The computational method for calculating standard error is very similar to that of standard deviation, with a slight difference in formula. The exact formula you use will depend on whether or not the population standard deviation is known. It’s also important to note that the following formulas can only be applied to data samples containing more than 20 values.

So, if the population standard deviation is known, you can use this formula to calculate standard error:

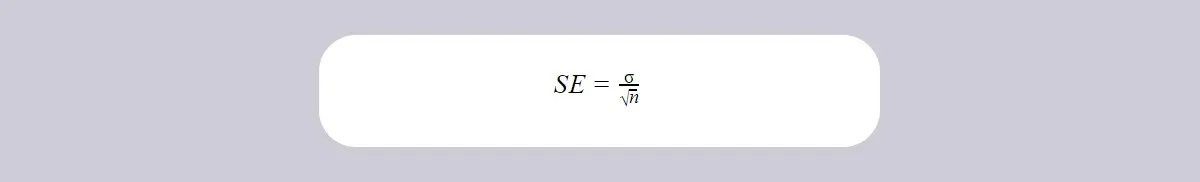
Where:

• SE refers to standard error of all possible samples from a single population
• σ refers to population standard deviation
• n refers to the number of values in the sample

If the population standard deviation is not known, use this formula: 

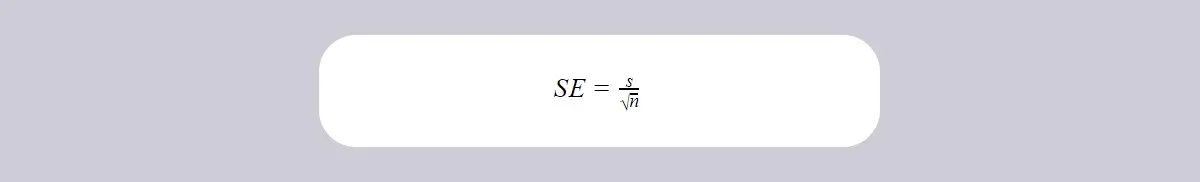
Where:

• SE refers to standard error of all possible samples from a single population
• s refers to sample standard deviation which is a point estimate of population standard deviation
• n refers to the number of values in the sample

How to calculate standard error (step by step)

Let’s break that process down step by step.

1. Find the square root of your sample size (n)
2. Find the standard deviation for your data sample (following the steps laid out in section three of this guide)
3. Divide the sample standard deviation (as found in step 2) by the square root of your sample size (as calculated in step 1)

Let’s solve a problem step-by-step to show you how to calculate the standard error of mean by hand.

How to calculate standard error with an example

Suppose a large number of students from multiple schools participated in a design competition. From the whole population of students, evaluators chose a sample of 300 students for a second round. The mean of their competition scores is 650, while the sample standard deviation of  scores is 220. Now let’s calculate the standard error.

1. Find the square root of the sample size. In our example,n = 300, and you can calculate the square root in Excel or Google Sheets using the following formula: =300^0.5. So n= 17.32
2. Find the standard deviation for your data sample. You can do this following the steps laid out in section three, but for now we’ll take it as known that the sample standard deviation S = 220.
3. Divide the sample standard deviation by the square root of the sample size. So, in our example, 220 / 17.32 = 12.7. So, the standard error is 12.7.

When reporting the standard error, you would write (for our example): The mean test score is 650 ± 12.7 (SE).

6. Standard error vs standard deviation: What’s the difference?

Now we know what standard deviation and standard error are, let’s examine the differences between them. The key differences are:

• Standard deviation describes variability within a single sample, while standard error describes variability across multiple samples of a population.
• Standard deviation is a descriptive statistic that can be calculated from sample data, while standard error is an inferential statistic that can only be estimated.
• Standard deviation measures how much observations vary from one another, while standard error looks at how accurate the mean of a sample of data is compared to the true population mean.
• The formula for standard deviation calculates the square root of the variance, while the formula for standard error calculates the standard deviation divided by the square root of the sample size.

7. Standard error vs standard deviation: When should you use which?

With those differences in mind, when should you use standard deviation and when should you use standard error?

Standard deviation is useful when you need to compare and describe different data values that are widely scattered within a single dataset. Because standard deviation measures how close each observation is to the mean, it can tell you how precise the measurements are. So, if you have a dataset forecasting air pollution for a certain city, a standard deviation of 0.89 (i.e. a low standard deviation) shows you that the data is precise.

Standard error is useful if you want to test a hypothesis, as it allows you to gauge how accurate and precise your sample data is in relation to drawing conclusions about the actual overall population. For example, if you want to investigate the spending habits of everyone over 50 in New York City, using a sample of 500 people, standard error can tell you how “powerful” or applicable your findings are.

8. Key takeaways and further reading

In this guide, we’ve explained how to calculate standard error and standard deviation, and outlined the key differences between the two. In summary, standard deviation tells you how far each value lies from the mean within a single dataset, while standard error tells you how accurately your sample data represents the whole population.

Statistical concepts such as these form the very basis of data analytics, so it’s important to get your head around them if you’re considering a career in data analytics or data science. If you’d like to try your hand at analyzing real data, we can recommend this free introductory data analytics short course. And, for more useful guides, check out the following:

• What’s the difference between covariance and correlation?
• What is exploratory data analysis?
• What is multivariate data analysis?