When it comes to working in data analytics—whether that’s as a data analyst or in a role that involves data in another capacity—there’s a long process involved, way before the actual analysis phase begins.
In fact, up to two-thirds of the time taken in the data analytics process is spent cleaning what’s known as “dirty” data: data that needs to be edited, worked on, or otherwise manipulated before it’s suitable for analysis.
During the cleaning phase, a data analyst may find outliers in the “dirty” data, which leads to either removing them from the dataset entirely, or handling them in another way. And so begs the question: what is an outlier?
If you’re interested, why not try CareerFoundry’s free, 5-day data analytics course? Otherwise, to skip ahead, just use the clickable menu:
- What is an outlier?
- How do outliers end up in datasets?
- How can you identify outliers?
- When should you remove outliers?
- Wrap-up and next steps
With that, let’s begin.
1. What is an outlier?
In data analytics, outliers are values within a dataset that vary greatly from the others—they’re either much larger, or significantly smaller. Outliers may indicate variabilities in a measurement, experimental errors, or a novelty.
In a real-world example, the average height of a giraffe is about 16 feet tall. However, there have been recent discoveries of two giraffes that stand at 9 feet and 8.5 feet, respectively. These two giraffes would be considered outliers in comparison to the general giraffe population.
When going through the process of data analysis, outliers can cause anomalies in the results obtained. This means that they require some special attention and, in some cases, will need to be removed in order to analyze data effectively.
There are two main reasons why giving outliers special attention is a necessary aspect of the data analytics process:
- Outliers may have a negative effect on the result of an analysis
- Outliers—or their behavior—may be the information that a data analyst requires from the analysis
Types of outliers
There are two kinds of outliers:
- A univariate outlier is an extreme value that relates to just one variable. For example, Sultan Kösen is currently the tallest man alive, with a height of 8ft, 2.8 inches (251cm). This case would be considered a univariate outlier as it’s an extreme case of just one factor: height.
- A multivariate outlier is a combination of unusual or extreme values for at least two variables. For example, if you’re looking at both the height and weight of a group of adults, you might observe that one person in your dataset is 5ft 9 inches tall—a measurement that would fall within the normal range for this particular variable. You may also observe that this person weighs 110lbs. Again, this observation alone falls within the normal range for the variable of interest: weight. However, when you consider these two observations in conjunction, you have an adult who is 5ft 9 inches and weighs 110lbs—a surprising combination. That’s a multivariate outlier.
Besides the distinction between univariate and multivariate outliers, you’ll see outliers categorized as any of the following:
- Global outliers (otherwise known as point outliers) are single data points that lay far from the rest of the data distribution.
- Contextual outliers (otherwise known as conditional outliers) are values that significantly deviate from the rest of the data points in the same context, meaning that the same value may not be considered an outlier if it occurred in a different context. Outliers in this category are commonly found in time series data.
- Collective outliers are seen as a subset of data points that are completely different with respect to the entire dataset.
Now we know what an outlier is, let’s take a look at how they end up in datasets in the first place.
2. How do outliers end up in datasets?
Now that we’ve learned about what outliers are and how to identify them, it’s worthwhile asking: how do outliers end up in datasets in the first place?
Here are some of the more common causes of outliers in datasets:
- Human error while manually entering data, such as a typo
- Intentional errors, such as dummy outliers included in a dataset to test detection methods
- Sampling errors that arise from extracting or mixing data from inaccurate or various sources
- Data processing errors that arise from data manipulation, or unintended mutations of a dataset
- Measurement errors as a result of instrumental error
- Experimental errors, from the data extraction process or experiment planning or execution
- Natural outliers which occur “naturally” in the dataset, as opposed to being the result of an error otherwise listed. These naturally-occurring errors are known as novelties
3. How can you identify outliers?
Now that you know how each type of outlier is categorized, let’s move on to figuring out how to identify them in your datasets. You can learn how to detect and handle them in our video seminar on outliers, presented by expert data scientist Dana Daskalova.
With small datasets, it can be easy to spot outliers manually (for example, with a set of data being 28, 26, 21, 24, 78, you can see that 78 is the outlier) but when it comes to large datasets or big data, other tools are required.
We’ll discuss some of the methods commonly used to identify outliers with visualizations or statistical methods, but there are many others available for implementation into your data analytics process. The method that you end up using will depend on the type of dataset you’re working with, as well as the tools you’re working with.
How to identify outliers using visualizations
In data analytics, analysts create data visualizations to present data graphically in a meaningful and impactful way, in order to present their findings to relevant stakeholders. These visualizations can easily show trends, patterns, and outliers from a large set of data in the form of maps, graphs and charts.
You can read more about the different types of data visualizations in this article, but here are two that a data analyst could use in order to easily find outliers.
Identifying outliers with box plots
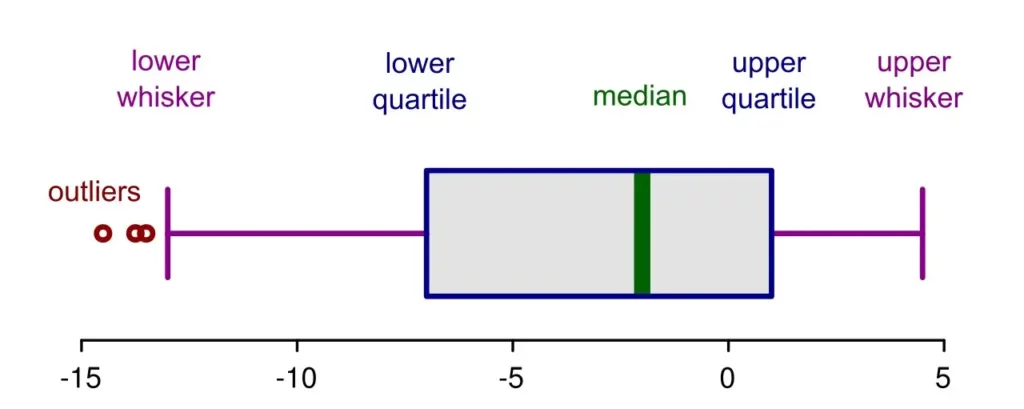
Visualizing data as a box plot makes it very easy to spot outliers. A box plot will show the “box” which indicates the interquartile range (from the lower quartile to the upper quartile, with the middle indicating the median data value) and any outliers will be shown outside of the “whiskers” of the plot, each side representing the minimum and maximum values of the dataset, respectively. If the box skews closer to the maximum whisker, the prominent outlier would be the minimum value. Likewise, if the box skews closer to the minimum-valued whisker, the prominent outlier would then be the maximum value. Box plots can be produced easily using Excel or in Python, using a module such as Plotly.
Identifying outliers with scatter plots
As the name suggests, scatter plots show the values of a dataset “scattered” on an axis for two variables. The visualization of the scatter will show outliers easily—these will be the data points shown furthest away from the regression line (a single line that best fits the data). As with box plots, these types of visualizations are also easily produced using Excel or in Python.
How to identify outliers using statistical methods
Here, we’ll describe some commonly-used statistical methods for finding outliers. A data analyst may use a statistical method to assist with machine learning modeling, which can be improved by identifying, understanding, and—in some cases—removing outliers.
Here, we’ll discuss two algorithms commonly used to identify outliers, but there are many more that may be more or less useful to your analyses.
Identifying outliers with DBSCAN
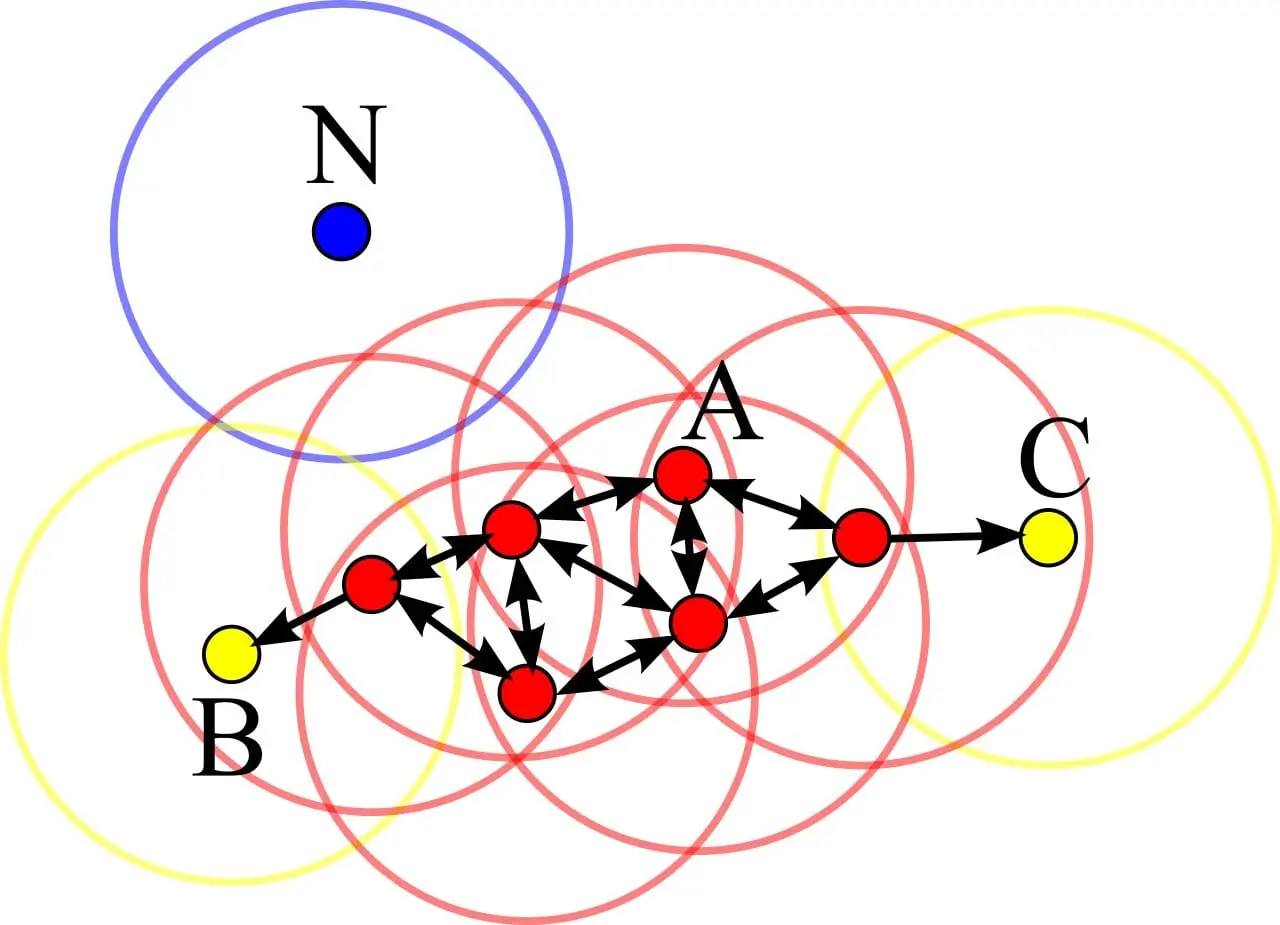
The above illustration is of a DBSCAN cluster analysis. Points around A are core points. Points B and C are not core points, but are density-connected via the cluster of A (and thus belong to this cluster). Point N is Noise, since it is neither a core point nor reachable from a core point.
DBSCAN (Density Based Spatial Clustering of Applications with Noise) is a clustering method that’s used in machine learning and data analytics applications. Relationships between trends, features, and populations in a dataset are graphically represented by DBSCAN, which can also be applied to detect outliers.
DBSCAN is a density-based clustering non-parametric algorithm, focused on finding and grouping together neighbors that are closely packed together. Outliers are marked as points that lie alone in low-density regions, far away from other neighbors.
Data analysts and those working with data mining and machine learning will surely come across DBSCAN—it’s an algorithm that’s been around since 1996 and, having won a ‘test of time award’ at a leading data mining conference, it seems like it’s going to remain an industry standard. Implementations of DBSCAN can be found on scikit, R, and Python.
Read more: What’s the Best Language for Machine Learning?
Identifying outliers by finding the Z-Score
Z-score—sometimes called the standard score—is defined on Wikipedia as “the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured.”
Computing a z-score helps describe any data point by placing it in relation to the standard deviation and mean of the whole group of data points. Positive standard scores appear as raw scores above the mean, whereas negative standard scores appear below the mean. The mean is 0 and standard deviation is 1, creating a normal distribution.
Outliers are found from z-score calculations by observing the data points that are too far from 0 (mean). In many cases, the “too far” threshold will be +3 to -3, where anything above +3 or below -3 respectively will be considered outliers.
Z-scores are often used in stock market data. Z-scores can be calculated using Excel, R and by using the Quick Z-Score Calculator.
Identifying outliers with the Isolation Forest algorithm
Isolation Forest—otherwise known as iForest—is another anomaly detection algorithm. The founders of the algorithm used two quantitative features of anomalous data points—that they are “few” in quantity and have “different” attribute-values to those of normal instances—to isolate outliers from normal data points in a dataset.
To show these outliers, the Isolation Forest will build “Isolation Trees” from the set of data, and outliers will be shown as the points that have shorter average path lengths than the rest of the branches.
Isolation Forest is used predominantly in machine learning. If you’d like to implement the algorithm into your analyses, implementation can be found—released by the algorithm’s founder— on SourceForge.
4. When should you remove outliers?
It may seem natural to want to remove outliers as part of the data cleaning process. But in reality, sometimes it’s best—even absolutely necessary—to keep outliers in your dataset.
Removing outliers solely due to their place in the extremes of your dataset may create inconsistencies in your results, which would be counterproductive to your goals as a data analyst. These inconsistencies may lead to reduced statistical significance in an analysis.
But what do we mean by statistical significance? Let’s take a look.
A quick introduction to hypothesis testing and statistical significance (p-value)
When you collect and analyze data, you’re looking to draw conclusions about a wider population based on your sample of data. For example, if you’re interested in the eating habits of the New York City population, you’ll gather data on a sample of that population (say, 1000 people). When you analyze this data, you want to determine if your findings can be applied to the wider population, or if they just occurred within this particular sample by chance (or due to another influencing factor). You do this by calculating the statistical significance of your findings.
This is part of hypothesis testing.
With hypothesis testing, you start with two hypotheses: the null hypothesis and the alternative hypothesis. Based on your findings and the statistical significance (or insignificance) of these findings, you’ll accept one of your hypotheses and reject the other. The null hypothesis states that there is no statistical significance between the two variables you’re looking at. The alternative hypothesis states the opposite.
Let’s explain with an example. Imagine you’re looking at the relationship between people’s self-esteem (measured as a score out of 100) and their coffee consumption (measured in terms of cups per day). These are your two variables: self-esteem and coffee consumption. When analyzing your data, you find that there does indeed appear to be a correlation (or a relationship) between self-esteem and coffee consumption. For instance, higher coffee consumption correlates with a higher self-esteem score. Is this a fluke finding? Or do people who drink more coffee really tend to have higher self-esteem?
To evaluate the strength of your findings, you’ll need to determine if the relationship between the two variables is statistically significant. There are several different tests used to calculate statistical significance, depending on the type of data you have. We won’t go into detail here, but essentially, you run the appropriate significance test in order to find the p-value.
The p-value is a measure of probability, and it tells you how likely it is that your findings occurred by chance. A p-value of less than 0.05 indicates strong evidence against the null hypothesis; in other words, there is less than a 5% probability that the results occurred by chance. In this case, your findings can be deemed statistically significant. If, on the other hand, your statistical significance test finds a p-value greater than 0.05, your findings are deemed statistically insignificant. They may have just occurred by chance.
Removing outliers without good reason can skew your results in a way that impacts the p-value, thus making your findings unreliable. So: it’s essential to think carefully before simply removing outliers from your dataset!
While evaluating potential outliers to remove from your dataset, consider the following:
- Is the outlier a measurement error or data entry error? If so, correct it manually where possible. If it’s unable to be corrected, it should be considered incorrect, and thus legitimately removed from the dataset.
- Is the outlier a natural part of the data population being analyzed? If not, you should remove it.
- Can you explain your reasoning for removing an outlier? If not, you should not remove it. When removing outliers, you should provide documentation of the excluded data points, giving reasoning for your choices.
If there is disagreement within your group about the removal of an outlier (or a group of outliers), it may be useful to perform two analyses: the first with the dataset intact, and the second with the outliers removed. Compare the results and see which one has provided the most useful and realistic insights.
5. Wrap-up and next steps
In this article, we’ve covered the basic definition of an outlier, as well as its possible categorizations. We then covered some commonly-used methods of identifying outliers, then discussed exactly how these outliers may end up in a dataset, and whether or not it’s appropriate to remove them in order to create useful insights for your organization.
Handling outliers is a fascinating and sometimes complicated process, which makes the world of data analytics all the more exciting! If you’d like to learn more about what it’s like to work as a data analyst, check out our free, 5-day data analytics short course.
You could also check out some of the other articles in our series about data analytics:

