Distribution is a core concept in data analytics, data science, and machine learning. It lays the foundation for statistical analysis of a given dataset, and provides the basis for certain machine learning models.
One of the most simple yet important types of distribution to get to grips with is Bernoulli distribution, named after the Swiss mathematician Jacob Bernoulli. In this post, we’ll provide a gentle but thorough introduction to Bernoulli distribution and Bernoulli trials. By the end, you’ll have a clear idea of what Bernoulli distribution actually means, and where it fits into the broader context of data analytics.
We’ll cover:
- What are distributions in statistics?
- What is Bernoulli distribution?
- Bernoulli distribution examples
- What are the conditions for Bernoulli distribution?
- Where does Bernoulli distribution come into data analytics, data science, and machine learning?
- Key takeaways and further reading
Before we dive into Bernoulli distribution, let’s first refresh on what distribution means in the world of statistics. If you’re already familiar with the concept of distribution, just skip ahead using the clickable menu.
1. What are distributions in statistics? A brief introduction
In statistics, a distribution is a function that shows the possible values for a variable and how often they occur within a given dataset. It enables you to calculate the probability of certain outcomes occurring, and to understand how much variation there is within your dataset.
Let’s imagine you’ve collected occupational data for 500 people living in New York. The different possible outcomes are all the various job titles within your dataset. Because occupation is categorical in nature (i.e. not numerical), the distribution of your dataset would tell you how many (or what percentage) of the people in your sample fall into each group. For example, 20% of the sample are lawyers, 10% are teachers, 5% are nurses, and so on.
With numerical data, the distribution will order the data from lowest to highest value. In this case, the distribution is presented as a graph or chart. The trained eye can then look at the shape of the graph to see, at a glance, how the data is distributed. A so-called normal distribution produces a symmetrical, bell-shaped curve on a graph. This indicates that most of the observations from the data cluster around the center (i.e. the mean value), with only a few, more extreme observations veering away from the mean in both directions. The normal distribution is also known as the Gaussian distribution or, based on the shape of the graph, the bell curve. Essentially, a normal distribution tells you that most observations (e.g. height) will fall within or close to the mean value, with just a few outliers.
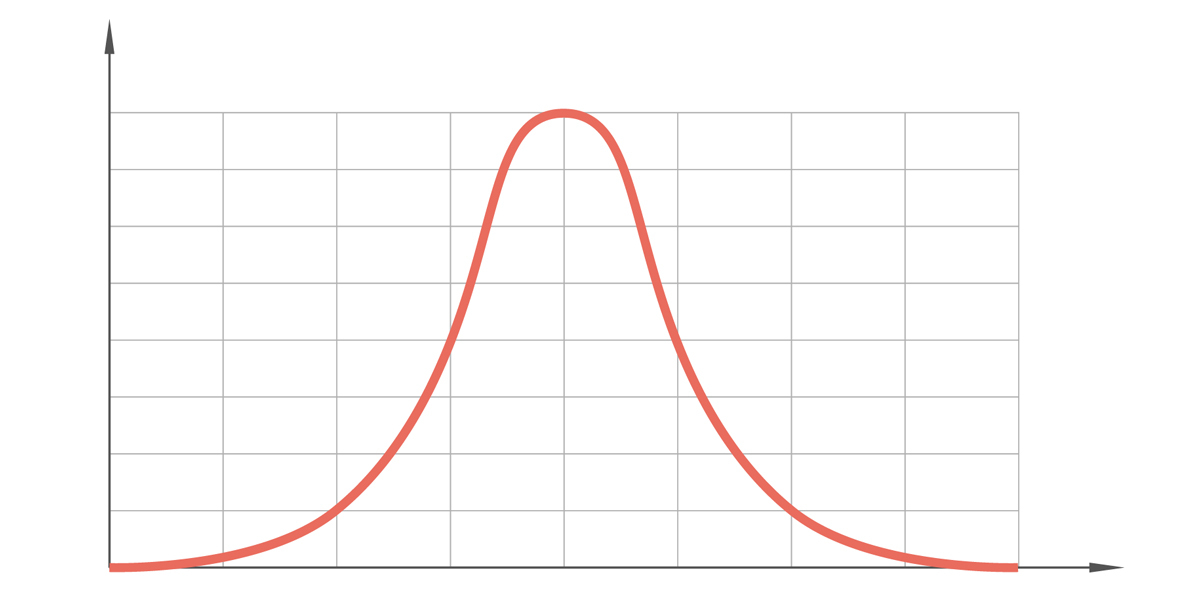
Normal distribution is just one of many different types of distributions. In this guide, we’ll focus on Bernoulli distribution.
2. What is Bernoulli distribution?
Bernoulli distribution is a discrete probability distribution, meaning it’s concerned with discrete random variables. A discrete random variable is one that has a finite or countable number of possible values—the number of heads you get when tossing three coins at once, or the number of students in a class.
So: A discrete probability distribution describes the probability that each possible value of a discrete random variable will occur—for example, the probability of getting a six when rolling a die. When dealing with discrete variables, the probability of each value falls between 0 and 1, and the sum of all the probabilities is equal to 1. So, in the die example, assuming we’re using a standard die, the probability of rolling a six is 0.167, or 16.7%. This is based on dividing 1 (the sum of all probabilities) by 6 (the number of possible outcomes).
That’s discrete probability distribution in a nutshell. So what about Bernoulli distribution?
Bernoulli distribution and Bernoulli trials explained
Bernoulli distribution applies to events that have one trial and two possible outcomes. These are known as Bernoulli trials. Think of any kind of experiment that asks a yes or no question—for example, will this coin land on heads when I flip it? Will I roll a six with this die? Will I pick an ace from this deck of cards? Will voter X vote “yes” in a political referendum? Will student Y pass their math test?
You get the idea. In Bernoulli trials, the two possible outcomes can be thought of in terms of “success” or “failure”—but these labels are not to be taken literally. In this context, “success” simply means getting a “yes” outcome (for example, rolling a six, picking an ace, and so on).
The Bernoulli distribution is, essentially, a calculation that allows you to create a model for the set of possible outcomes of a Bernoulli trial. So, whenever you have an event that has only two possible outcomes, Bernoulli distribution enables you to calculate the probability of each outcome.
What’s the difference between Bernoulli distribution and binomial distribution?
While grappling with Bernoulli distribution, you’ve likely come across another term: binomial distribution. So what’s the difference between the two, and how do they relate to one another?
In very simplistic terms, a Bernoulli distribution is a type of binomial distribution. We know that Bernoulli distribution applies to events that have one trial (n = 1) and two possible outcomes—for example, one coin flip (that’s the trial) and an outcome of either heads or tails. When we have more than one trial—say, we flip a coin five times—binomial distribution gives the discrete probability distribution of the number of “successes” in that sequence of independent coin flips (or trials).
So, to continue with the coin flip example: Bernoulli distribution gives you the probability of “success” (say, landing on heads) when flipping the coin just once (that’s your Bernoulli trial). If you flip the coin five times, binomial distribution will calculate the probability of success (landing on heads) across all five coin flips.
That’s a very simplistic overview—you’ll find a more detailed explanation of binomial distribution here. For now, let’s return to Bernoulli distribution with some examples.
3. Examples of Bernoulli distribution
Bernoulli distribution example: Tossing a coin
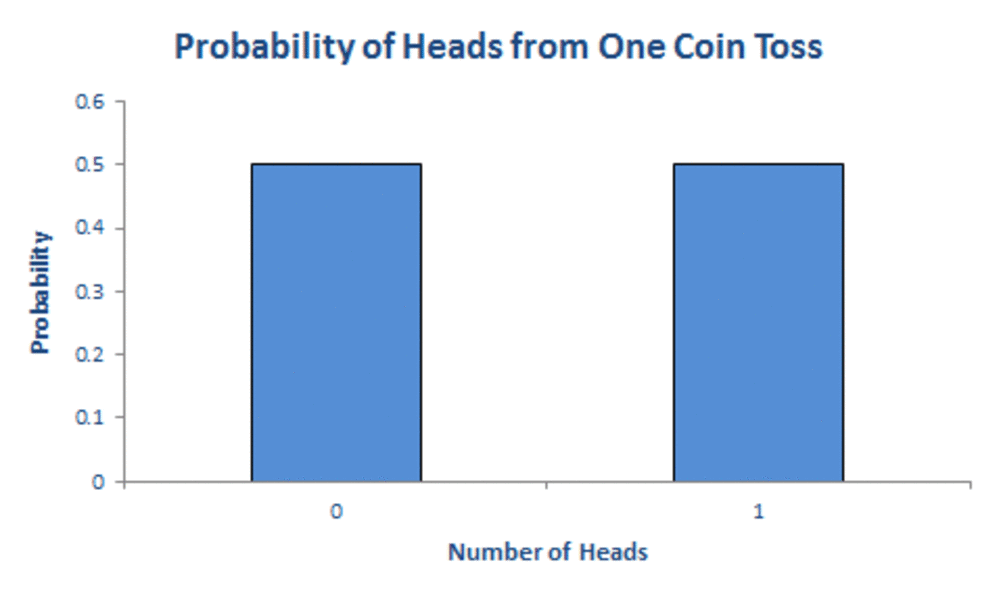
The coin toss example is perhaps the easiest way to explain Bernoulli distribution. Let’s say that the outcome of “heads” is a “success,” while an outcome of “tails” is a “failure.” In this instance:
- The probability of a successful outcome (landing on heads) is written as p
- The probability of a failure (landing on tails), written as q, is calculated as 1 **–** p
With a standard coin, we know that there’s a 50/50 chance of landing on either heads or tails. So, in this case:
- p = 0.5
- q = 1– **0.5
So, in our coin toss example, both p and q = 0.5. On a graph, you’d represent the probability of a failure as “0” and the probability of success as “1,” both on the y-axis.
Further examples of Bernoulli distribution
The coin-toss example is a very simple one, but there are actually many scenarios in life that have a yes-no outcome. For example:
- Will you pass or fail a test?
- Will your favorite sports team win or lose their next match?
- Will you be accepted or rejected for that job you applied for?
- Will you roll a six in the opening round of your favorite board game?
- Will you win or lose the lottery?
In this article, Swizec Teller explains how Bernoulli trials and Bernoulli distribution can help you figure out how many job applications you need to send out before you get a job. Bernoulli distribution is also used in medicine and clinical trials to model the success rate of a certain drug or the outcome of a clinical trial. For example, when developing a new drug, pharmaceutical scientists can use Bernoulli distribution to calculate the probability that a person will be cured or not cured with the help of the new drug. Bernoulli distributions are also used in logistic regression to model the occurrence of disease. You can learn more about logistic regression in this post.
4. What are the conditions for Bernoulli distribution?
To help you understand when and how Bernoulli distribution applies, it’s useful to consider the conditions for Bernoulli trials. An event or experiment can only be considered a Bernoulli trial (and thus be relevant for Bernoulli distribution) if it meets these criteria:
- There are only two possible outcomes from the trial. Another way to think of this is in terms of “success” or “failure”—in other words, does your experiment ask a “yes or no” question? Think back to our previous examples, such as “Will student X pass their math test?” or “Will patient Y be cured when they take this drug?”
- Each of the two outcomes has a fixed probability of occurring. In other words, no matter how many times you flip a coin, the probability of landing on heads is fixed. In mathematical terms, the probability of success is always p, and the probability of failure is always 1 – p.
- Trials are entirely independent of each other. The result of one trial (say, the first coin flip) has absolutely no bearing on the outcome of any subsequent coin flips.
If a scenario meets all three of those criteria, it can be considered a Bernoulli trial. Now we’re familiar with Bernoulli distribution, let’s consider where it comes into play in the broader fields of data analytics, data science, and machine learning.
5. Bernoulli distribution in data analytics, data science, and machine learning
Probability distributions, such as Bernoulli distribution, are not only useful for mathematicians and statisticians; they also have a crucial role to play in data analytics, data science, and machine learning. Data analysts and data scientists work with large volumes of data, and looking at the distribution of a given dataset is an essential part of exploratory data analysis—that is, getting an initial understanding of your data before you investigate further.
In machine learning, many models work based on distribution assumptions, and the Bernoulli distribution (and other discrete probability distributions) are primarily used in the modeling of binary and multi-class classification problems. Some examples of binary classification models include spam filters which detect whether an email should be classified as “spam” or “not spam,” models that can predict whether a customer will take a certain action or not, or classifying a product as, say, a book or a film. An example of a multi-class classification model could be a model that identifies which category of products will be most relevant to a particular customer.
As one of the more simple distributions, Bernoulli distribution often serves as a starting point for more complex distributions. For example, the Bernoulli process lays the foundation for binomial distribution, geometric distribution, and negative binomial distribution—all of which play a crucial role in deep learning. You can learn more about deep learning (and how it differs from machine learning) in this guide.
So, if you’re keen to delve deeper into data analytics, data science, or machine learning, probability distributions, like the Bernoulli distribution, are a good place to start.
6. Key takeaways and further reading
In this post, we introduced Bernoulli distribution—a concept worth getting to grips with if you’re considering a career in any kind of data-related field. To recap:
- Bernoulli distribution is a discrete probability distribution
- It describes the probability of achieving a “success” or “failure” from a Bernoulli trial
- A Bernoulli trial is an event that has only two possible outcomes (success or failure). For example, will a coin land on heads (success) or tails (failure)?
- Bernoulli distribution is a type of binomial distribution
If you’re learning about statistics with a view to getting started in the data industry, why not try out a free introductory data analytics short course? And, for more introductory guides, check out the following:
